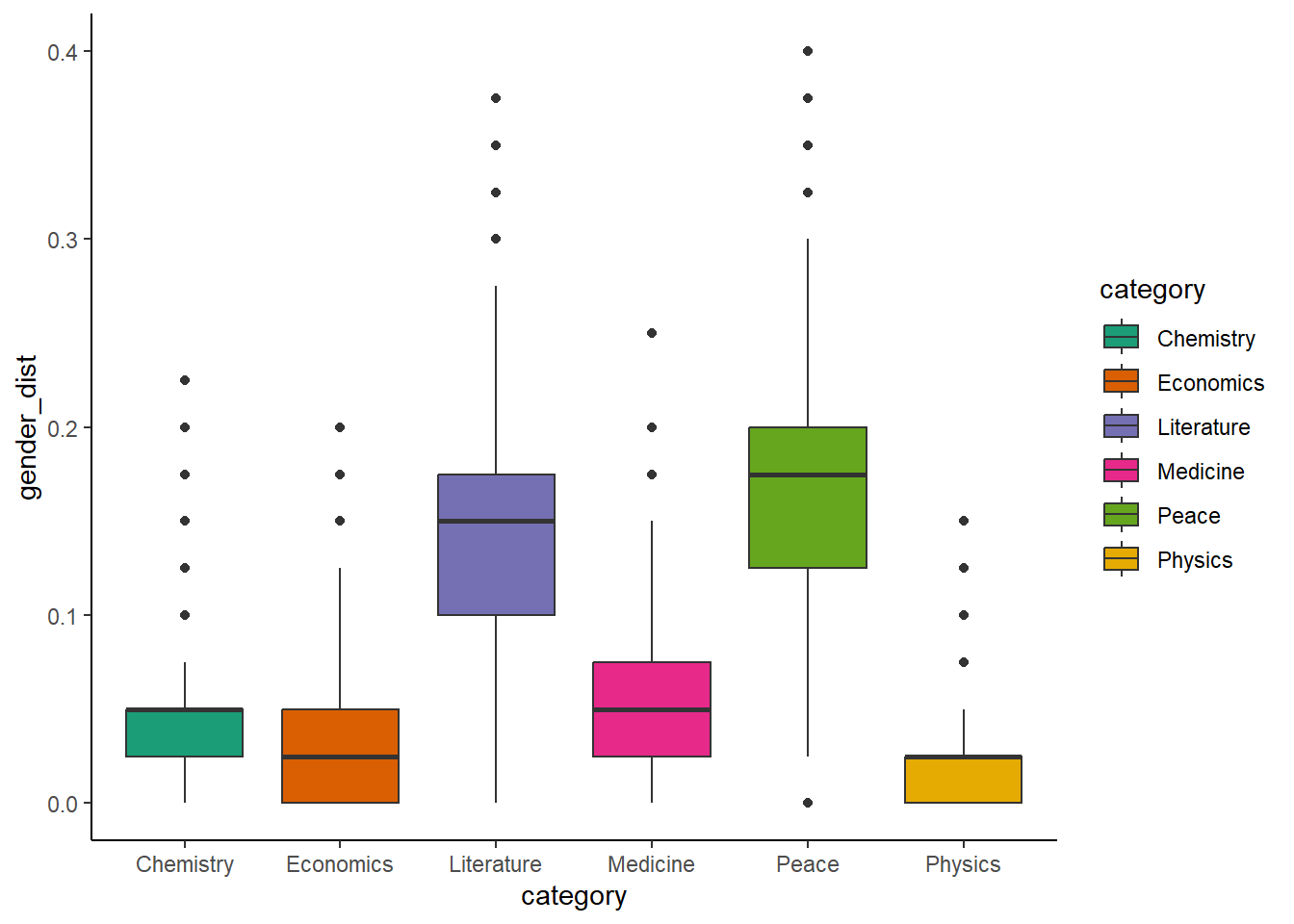Introduction
Gender representation in the Nobel Prizes has long been a subject of scrutiny and debate, reflecting broader societal trends and challenges in achieving gender equality. Since the establishment of the Nobel Prizes in the late 19th century, gender has been a forefront of the critiques of the institution, with a significant under representation of women laureates across various categories. The prizes, which recognize outstanding achievements in fields such as physics, chemistry, literature, peace, and medicine, have historically seen a disproportionate number of male laureates; striking up conversations about women’s contributions to those fields and prize winners. This discrepancy has sparked discussions about the systemic barriers and biases that may contribute to the limited recognition of women despite their notable contributions to science, literature, and peace.
Despite progress in recent decades and an increasing number of women making groundbreaking contributions in traditionally male-dominated fields, the Nobel Prizes’ slow pace of change in achieving gender parity is noticeable in contrast to gains in other spheres. Efforts to address this issue have involved raising awareness about the gender gap, advocating for equal opportunities in education and research, and encouraging the nomination of more women for consideration. As discussions surrounding gender representation gain momentum globally, the Nobel Committee faces ongoing pressure to reassess its selection processes and criteria to ensure a fair and inclusive recognition of achievements, irrespective of gender. The exploration of gender representation in the Nobel Prizes sheds light as a lens by which to understand the plight of women in academia, science, and other fields, highlighting the need for continued efforts to dismantle systemic barriers and foster an environment that recognizes and rewards excellence across all levels, regardless of gender.
The larger societal conversation deserves better understanding of gender representation within the prestigious realm of Nobel Prizes, a void I hope to complete through this paper. I will delve into the statistics of gender distribution across all prize categories, prompting an exploration into the extent of women’s representation and potential variations among the diverse fields; variations which may expose deeper structural critiques. I aim to discover whether certain categories exhibit a more equitable gender balance than others, and crucially, how this representation has evolved over time. Adding a temporal dimension introduces a dynamic perspective, allowing for an investigation into whether strides have been made in achieving gender parity or whether persistent disparities persist.
The exploration of gender representation necessitates a careful capturing of each category, unveiling potential nuances that might be obscured when analyzing the dataset as a whole. For instance, does the gender distribution of Physics winners exhibit a different trajectory when compared to Literature? Are there any discernible patterns that shed light on the evolving landscape of recognition in Medicine, Peace, or any other category? By investigating these individual categories, a more granular understanding of gender representation can be found, contributing to a comprehensive and insightful analysis.
As I embark on this lofty task, I hope to not only comprehend the current state of affairs but also to lead the way for future discourse around representation and how societies recognize and reward high achievers. This comprehensive approach promises to contribute valuable insights to the broader discourse on diversity, recognition, and the evolving nature of excellence in various domains.
Data Acquisition and Cleaning
My first step in answering these questions was to gather a suitable dataset for the task. Having extensive experience with its interface, I learned first towards searching Kaggle. Kaggle itself is a widely recognized platform that serves as a hub for data science and machine learning enthusiasts, offering a diverse array of datasets for exploration, analysis, and model development. The platform’s datasets are open sourced and contributed to by a vibrant community of data scientists, researchers, and organizations, covering an extensive range of topics and domains.
To search for a suitable dataset exploration for my project, I began by navigating to the Kaggle website and started with the “Datasets” section where I search for reputable databases based on categories, tags, and popularity. I also used specific keywords to narrow down my focus and discover datasets aligned with my interests.
After a couple of minutes on Kaggle, I came across a comprehensive dataset that spans the years from 1901 to 2023, offering a wealth of information on Nobel Prize recipients. This dataset was a treasure trove for my project, providing valuable insights into the demographics, achievements, and background of individuals who have made significant contributions in various fields and were awarded for their contributions. The temporal scope of the dataset, covering over a century of Nobel Prize history and every recipient since its creation, presents an excellent opportunity to analyze and understand trends and patterns in the distribution of awards over time.
One of the standout features of this dataset was also its inclusion of diverse variables, offering a multifaceted view of each Nobel Prize recipient. Beyond just gender representation, the dataset encompassed additional dimensions of analysis. For instance, it provides information on the number of participants who received each award, shedding light on collaborative efforts and shared recognitions.
Moreover, the dataset delves into the age of the participants, offering intriguing insights into the relationship between age and the likelihood of receiving a Nobel Prize. This temporal aspect adds a dynamic dimension to the study, enabling researchers to explore whether certain age groups are more likely to be recognized for their contributions in specific categories.
There was also geographical information included in the dataset, detailing where each participant is from.Additionally, the dataset’s inclusion of a description outlining why each recipient received the award opens up avenues for text based analysis for future work, allowing researchers to delve into the motivations and criteria behind each recognition. While not as necessary for the overarching questions on gender representation, these excess variables became a strong grounding point for understanding the pool of recipients and common traits between them.
In essence, this Kaggle dataset not only encapsulates a vast array of information about Nobel Prize recipients but also provides a holistic view of their contributions, contexts, and demographics. I was committed to using it as my dataset and began the process of bringing it to my machine for cleaning and for uncovering nuanced insights into the dynamics of achievement and recognition in the academic and scientific realms over the past century.
The dataset preparation process for this analysis was relatively streamlined, as a significant portion of the data had undergone preprocessing and was formatted dutifully. The cleaning steps primarily involved transforming the gender variable into a binary numeric value, facilitating regression modeling and allowing for numeric summaries of gender distribution around crosstab rates. Additionally, I decided to remove any organizations that had received awards from the dataset in a logical step, especially when the focus is on individual gender representation. This ensures that the analysis centers on the recognition and representation of individuals rather than organizational entities and so I do not accidentally misgender those who worked in those organizations. Another noteworthy aspect of the data preparation process was the formatting of birth years to ensure consistency and make age calculations far simpler.
Moreover, the characteristics of the dataset made it analytically convenient for my analysis due to a couple factors. The independence of data points was one, as the years in which Nobel Prizes are awarded and who is awarded them over categories do not have a direct influence on each other. Each year’s laureates are determined independently and the disparate nature of categories with a broad spectrum of fields, providing insights into gender representation across various domains without any overlap which would violate independence.
I would like to expand upon this further as assumption of independence in statistical analysis is crucial for valid interpretation of results. In the context of Nobel Prize data, several factors contribute to the statistical independence of the data points which will be used. Here are a few reasons:
Annual Selection Process: The Nobel Prizes are awarded annually in various categories, such as Physics, Chemistry, Medicine, Literature, Peace, and Economic Sciences. Each year, the Nobel Committees independently evaluate and select laureates based on their achievements or contributions during that specific year. The decisions for one year’s prizes are typically made without direct influence from or consideration of the decisions made in previous or subsequent years.
Changing Nominations: The pool of nominees for Nobel Prizes changes each year. New individuals or organizations are nominated, and the selection committees consider their contributions within the context of the current year. This variability in the pool of nominees contributes to the independence of the data across years.
Different Fields and Criteria: Nobel Prizes are awarded in distinct fields, each with its own set of criteria and evaluative measures. The considerations for awarding a Nobel Prize in Physics, for instance, would be independent of the considerations for a Nobel Prize in Literature. This separation of fields and criteria reinforces the independence of the data across different Nobel Prize categories.
Randomness in Achievements: Scientific and literary achievements, as well as contributions to peace, are often driven by a multitude of factors, including individual efforts, geopolitical events, and societal developments. These factors are dynamic and can change from year to year, contributing to the randomness and independence of Nobel Prize data across different years.
It’s important to note that while the individual selections within a given year may be independent, there could be broader trends or patterns that emerge over longer periods, and these might be subject to bias which may be captured in the analysis. Additionally, the Nobel Prize council is subject to human judgment and can be influenced by societal, political, or cultural contexts to some extent although good faith will be extended for this research project.
This dataset’s inherent characteristics, coupled with the systematic cleaning and formatting steps taken by myself and those on kaggle, position it as a robust foundation for in-depth analyses of gender representation in Nobel Prize recipients. The thoughtful preprocessing will not only streamline the analytical process but also ensure the reliability and accuracy of the insights derived from the data, answering suitable questions about gender representation.
Data Exploration
While delving into the nuanced details of Nobel Prize recipient demographics, the dataset revealed a fascinating panorama of statistics and facts which provide insight into the body as a whole. Primarily, a notable gender discrepancy emerges, with 64 women and approximately 900 men having received Nobel prizes. This discrepancy easily underscores the historical underrepresentation of women in these prestigious accolades even up to the modern day and acts as a schism which I hope to understand.
Another factual statement noticed was a significant milestone that occurred in 2023, the year where women received the largest share of awards. This shift could signify a positive trend towards greater gender inclusivity in Nobel Prize awardees in the modern world, reflecting advancements in the acknowledgment of diverse contributions across various fields.
The geographical distribution of laureates also added another layer to the narrative. The United States emerged as the most common country of origin, contributing to 29 percent of Nobel Prize recipients. This dominance emphasizes the profound impact of American researchers, scholars, and professionals on the global stage, although the gender representation of this group implied that on average American women won fewer overall awards compared to men from the country. Within the United States, New York stands out as the most common city of origin, boasting 6 percent of Nobel laureates. This regional concentration adds an interesting facet to the exploration of Nobel Prize demographics.
The dataset also provides intriguing insights into the age distribution of recipients. On average, laureates were approximately 60 years old, with notable outliers such as the oldest recipient, John Goodenough, who received a Nobel Chemistry Award at the remarkable age of 97. Conversely, the youngest recipient, Malala Yousafzai, received a Nobel Peace Prize at the age of 17. These age extremes offer a dynamic perspective on the span of achievements recognized by the Nobel Committee and how the requirements might vary across categories.
Examining the distribution of awards across categories unveils notable patterns. Physics awards emerged as the most frequently bestowed, reflecting the significant contributions and advancements in the field. On the contrary, Economic awards have been the least conferred, possibly reflecting the stringent criteria or infrequent groundbreaking contributions in this domain.
In essence, this detailed exploration of Nobel Prize demographics unveils a mosaic of trends, achievements, and disparities. As we traverse the historical trajectory of Nobel recognitions, these insights not only illuminate the remarkable accomplishments of laureates but also prompt contemplation on the evolving nature of recognition, diversity, and excellence in the realms of science, literature, peace, and beyond.
Data Analysis
In the quest to unravel the intricate tapestry of gender representation within the esteemed cohort of Nobel Prize recipients, employing robust analytical techniques becomes necessary to show verifiable trends. This section delves into the methodological approaches harnessed to dissect, scrutinize, and comprehend the nuanced patterns governing the gender distribution across various Nobel Prize categories. Analyzing such a multifaceted data will involve a strategic blend of independence tests, regression modeling, and bootstrap methods to paint an accurate and comprehensive picture of how gender representation has evolved over time and within distinct academic and scientific categories. From statistical measures to temporal trends, this section will work to explain the methodologies harnessed to capture and interpret the intricate situation of gender in the Nobel Prize landscape.
Chi Squared Test
The chi-squared test is the first statistical method I will use to determine if there is a significant association between a suite of categorical variables. The test is based on the comparison of observed and expected frequencies within a contingency table, which is a matrix that displays the distribution of data across different categories for each variable. The chi-squared test assesses whether the differences between the observed and expected frequencies are statistically significant, providing insights into the independence or dependence of the variables and features in the contingency table.
The test is applied by first formulating a null hypothesis that assumes no association between the variables. Subsequently, the observed frequencies from the data are compared to the frequencies that would be expected under the assumption of independence. The calculation involves computing the chi-squared statistic, which quantifies the overall discrepancy between observed and expected values. The resulting statistic is then compared to a chosen or formulated critical value from the chi-squared distribution with degrees of freedom determined by the dimensions of the contingency table itself. If the calculated chi-squared statistic exceeds the critical value, the null hypothesis is rejected, indicating that there is a significant association between the variables.
Chi-squared tests find applications in various fields, including biology, social sciences, and market research. For example, it can be used to assess if there is a significant relationship between gender and voting preferences, or whether there is an association between the occurrence of a genetic trait and exposure to a certain environmental factor. Despite its widespread use, it’s essential to interpret the results cautiously and consider the assumptions of the test, and will work well to calculate the independence of observations across Nobel prize categories for our data.
Regression
In order to check for increases in gender representation over time, I will also be using a regression model. Linear regression is a statistical method used to model a linear relationship between a dependent variable and one or more independent variables by fitting a linear equation to the observed data. The goal of linear regression is to find the best-fitting line that minimizes the sum of the squared differences between the predicted values and the actual values of the dependent variable. The resulting linear equation takes the form of \((Y = b_0 + b_1X_1 + b_2X_2 + \ldots + b_nX_n)\), where \((Y)\) is the dependent variable, \((X_1, X_2, \ldots, X_n)\) are the independent variables, and \((b_0, b_1, b_2, \ldots, b_n)\) are the coefficients representing the intercept and slopes.
The coefficients are estimated using a method called the least squares, which aims to minimize the sum of the squared residuals, the differences between the observed and predicted values. The resulting linear regression equation can be used to make predictions or understand the strength and direction of the relationships between variables. The coefficient \((b_1)\), for instance, represents the change in the dependent variable for a one-unit change in the corresponding independent variable, assuming that all other variables remain constant.
Linear regression is widely applied in various fields and will be used in conjunction with year and category in my model. To mention it quickly, linear regression assumes a linear relationship between variables, it’s essential to assess the model’s assumptions and potential limitations, such as the presence of outliers or the need for more complex models when dealing with non-linear relationships.
Bootstrapping Means
After establishing independence and trends with those previous models, I will use bootstrapping to find the ‘true’ gender distributions of categories for ranking. Bootstrapping is a resampling technique used to estimate the distribution of a statistic by repeatedly sampling, with replacement, from the observed data. This method is particularly valuable when dealing with small datasets, like the 1000 variables for Nobel prize winners, as it provides a way to assess the variability of a statistic, such as the mean, even when the sample size is limited. For each of these samples, the mean is calculated, resulting in a distribution of means that represents the variability in estimating the population mean from the available data.
This secondary data based on the means of the sampled group will actually be normally distributed due to the properties imbued by the central limit theorem. The Central Limit Theorem itself is a fundamental concept in statistics that describes this very distribution of sample means. It states that, regardless of the shape of the original population distribution, the distribution of sample means will be approximately normal if the sample size is sufficiently large. In simpler terms, as you repeatedly draw random samples from a population and calculate their means, those means will converge to a normal distribution.
The central limit theorem is key when bootstrapping as, through the process of repeatedly resampling with replacement, the distribution of the sample mean generated by bootstrapping approaches a normal distribution, even if the original data is not normally distributed. This is especially relevant when making inferences about the population mean or constructing confidence intervals. This normal distribution will set up a further ANOVA test which requires normally distributed data as one of its assumptions
This technique is especially useful in situations where assumptions of normality may be questionable or when the sample size is too small for conventional statistical methods. Additionally, bootstrapping provides valuable insights into the stability of the estimated mean and can help identify potential sources of bias or outliers in the data. However, it’s essential to keep in mind that while bootstrapping is a powerful and versatile technique, its effectiveness is still contingent on the representativeness of the original dataset and the potential presence of systematic biases.
ANOVA test
the ANOVA test I mentioned, or the Analysis of Variance test, is a statistical technique used to assess whether there are any statistically significant differences between the means of three or more independent groups. ANOVA works by partitioning the total variance in a dataset into different components: variance between groups and variance within groups. The test then evaluates whether the variance between groups is significantly larger than the variance within groups. If the variance between groups is significantly greater, it suggests that there are significant differences in the means of the groups.
ANOVA is particularly useful when comparing means across multiple groups, such as the nobel prize categories, rather than conducting pairwise comparisons, which can increase the risk of Type I errors. As alluded to earlier, One of the critical assumptions of ANOVA is the homogeneity of variances, meaning that the variance within each group should be approximately equal. Violations of this assumption can affect the validity of the results. ANOVA also assumes that the observations within each group are independent and that the data are normally distributed. If these assumptions are not met, alternative methods or transformations may be considered.
ANOVA is a powerful and widely used statistical tool for comparing means across multiple groups and it will act as an updated version of our Chi squared test to see if there are still differences across categories. It will provide a comprehensive assessment of whether there are significant differences in the population means, helping me to make informed conclusions about the effects of category on gender representation.
Results
With all of the methods summarized, I will go through the steps and results of my analysis.
Warning: package 'tidyverse' was built under R version 4.3.2
Warning: package 'ggplot2' was built under R version 4.3.3
Warning: package 'tidyr' was built under R version 4.3.2
Warning: package 'readr' was built under R version 4.3.2
Warning: package 'dplyr' was built under R version 4.3.2
Warning: package 'stringr' was built under R version 4.3.2
Warning: package 'lubridate' was built under R version 4.3.2
Chi Squared Test
In navigating the intricate landscape of gender distributions among the Nobel Prize categories, a fundamental question takes center stage: do these distributions operate independently of one another? This pivotal inquiry sheds light on whether the representation of gender within a specific category is influenced by or independent of the dynamics observed in other categories. The analytical tool best fitted to answer this question is the chi-squared test, a robust statistical method designed to assess the association between categorical variables. This statistical methodology allows us to discern patterns, associations, and potential dependencies within the dataset, providing a rigorous framework for understanding the intricate relationships among different categories.
As a starting point, the analysis will present a comprehensive contingency table, the source from which the numeric counts for the test are sourced. This table forms the basis for the subsequent chi-squared test, delineating the frequencies of gender representation within each Nobel Prize category.
chemistry economics literature medicine peace physics
female_count2 8 3 17 13 19 4
male_count2 183 90 103 214 92 219
Upon initial analysis of the table, a pattern emerges in the distribution patterns between male and female recipients across various Nobel Prize categories. Women, while overall lacking in representation, are more prevalent in some groups rather than others. The upcoming chi-squared test will leverage a comprehensive count table as its foundational framework, systematically examining the distributions across each column. This test has a null hypothesis, positing that the columns are not independent and are drawn from the same distribution. In direct contrast, the alternative hypothesis contends that the data does not reflect being sourced from a single distribution, suggesting potential independence among the columns.
I would like to elaborate on the alternative hypothesis by emphasizing that it does not assert independence among all columns. Rather, it points to the likelihood that at least one column exhibits variations, indicating potential disparities in gender representation overall. However, more than one column could deviate from the expected distribution. As we proceed, the chi-squared test will be executed, and the output analyzed in context. This statistical approach promises not only to unveil insights into the relationships and distinctions among gender distributions across Nobel Prize categories but also to provide a robust foundation for understanding the nuanced patterns inherent in the representation of male and female recipients.
Pearson's Chi-squared test
data: count_table
X-squared = 43.023, df = 5, p-value = 3.655e-08
With a p-value of .00000007855 derived from the chi-squared test we can unequivocally reject the null hypothesis and embrace the alternative hypothesis. This statistical evidence compellingly indicates that there exists significant variability in the distribution of Nobel Prize categories when considering gender. This serves as a robust foundation, substantively confirming that gender representation across Nobel Prize categories is not uniform. Each category exhibits distinctive characteristics, thereby laying a profound groundwork for further exploration.
The ensuing sections, notably bootstrapping and ANOVA, will delve into the nuanced implications of this fact and will expand upon the behavior with specificity and interest. The journey ahead involves expanding upon this foundational conclusion, unraveling the subtleties of the observed differences, and extracting meaningful insights that transcend statistical significance. I hope this shows a trend which can be seen to continue throughout the rest of the research.
Regression
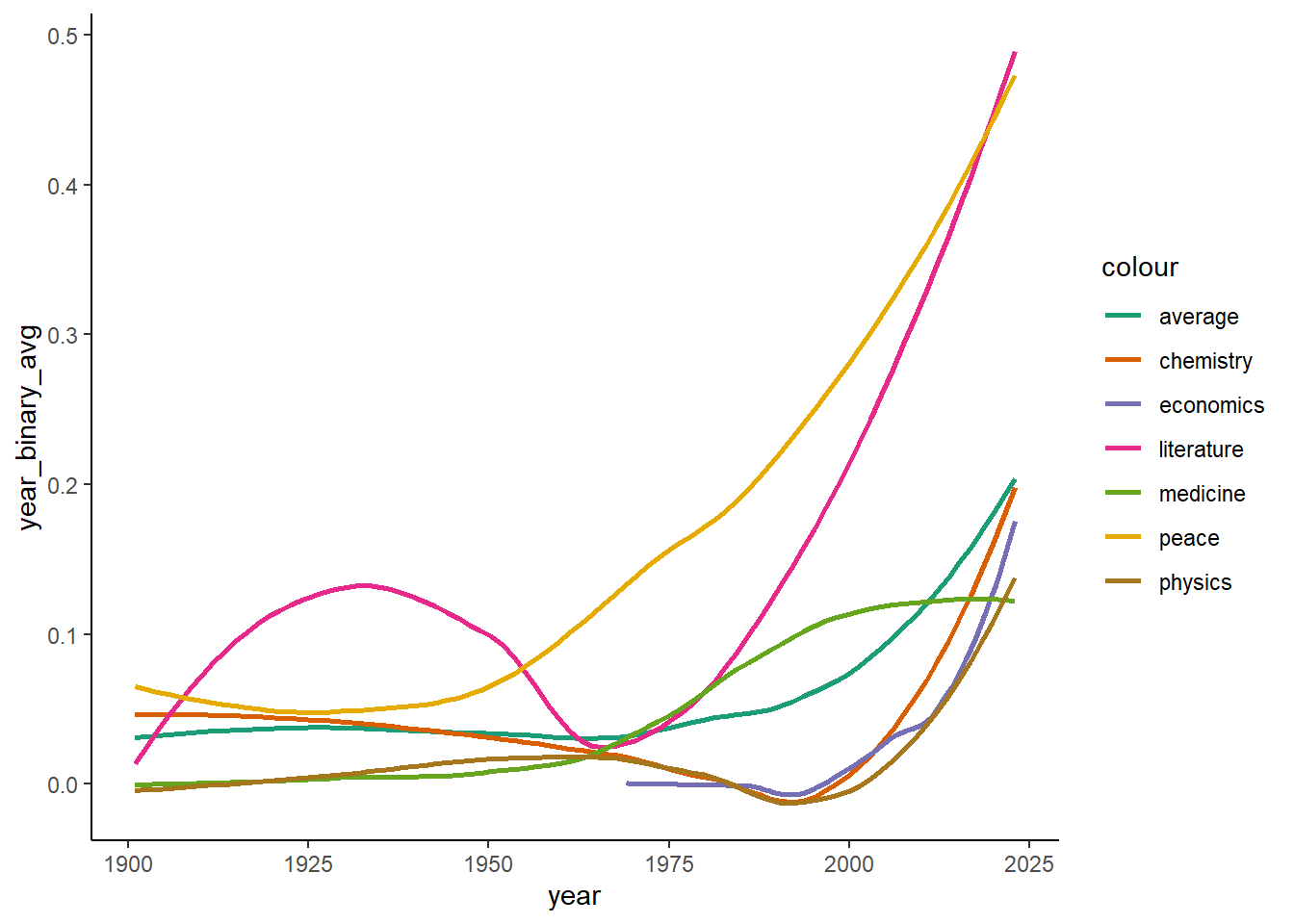
The next phase of our analysis entails the application of regression as a robust statistical tool to ascertain whether significant differences exist across categories, years, and the interplay of these two factors. This multifaceted approach seeks to unravel the dynamic relationships and potential trends inherent in the representation of women among Nobel Prize recipients. To aid in this analysis, I will create a visualization that encapsulates the evolving representation of women over time. This graphical representation serves not only as a descriptive tool but also as a precursor to the subsequent regression model, offering an insightful prelude to the statistical nuances that will come with the model.
Moving forward, the regression model will meticulously assess the statistical behavior of women’s representation, examining how categories, years, and their interaction contribute to the observed variations. This strategic integration of visualization and regression sets the stage for a comprehensive understanding of the intricate dynamics at play and paves the way for insightful interpretations that can provide more insights than either would have provided on their own.
The previous graph implied a discernible upward trajectory that was evident in recent years, with literature and peace categories markedly outpacing the overall average, which was represented by a dark green line in the graph. These contemporary surges signify a noteworthy shift in gender dynamics, with representation nearing 50% in certain fields. This surge implied a progressive trend in recent times, which gives evidence of hope in the longer trends going towards the future.
There are a couple of other distinctive features in the graph which I would like to discuss. There was a notable dip in literature during the 1960s and a similar low point in the 1990s for chemistry, economics, and physics. The disparities between the inaugural years in the 1900s and the subsequent periods further underscore the evolving nature of women’s recognition in the Nobel Prize arena with some gains and losses amongst all of the categories.
While the graph captures nuanced patterns, it also hints at the dynamic responsiveness of certain categories to changing gender dynamics. The distinctions observed suggest that some prizes may exhibit greater flexibility and a propensity to adapt swiftly to the increasing representation of women in their respective fields. This adaptability is particularly pronounced in the modern-day landscape, wherein certain categories stand out by rising faster or more comprehensively than others.
As we transition to the statistical realm, these visual relationships form the basis for our expectations of the model. While the relationships observed in the graph may not strictly adhere to linear trends, the stage is set for an expected statistical increase in women’s representation over time. Additionally, the graph hints at inherent differences across categories, with peace and literature emerging as categories likely to foster a higher likelihood of female Nobel Prize recipients. This anticipation forms a compelling hypothesis that will be rigorously tested and validated through our upcoming regression analyses.
Call:
lm(formula = gender_binary ~ year + category + prizeShare + age_of_award +
year * category, data = gender_data2)
Residuals:
Min 1Q Median 3Q Max
-0.35839 -0.07824 -0.04184 -0.00623 0.99676
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.3635254 1.0572748 -1.290 0.19748
year 0.0007723 0.0005443 1.419 0.15625
categoryeconomics -3.0337404 3.2607807 -0.930 0.35241
categoryliterature -2.9499632 1.5902324 -1.855 0.06390 .
categorymedicine -1.6306180 1.3791577 -1.182 0.23737
categorypeace -3.7446118 1.6169587 -2.316 0.02078 *
categoryphysics -0.3611362 1.3405715 -0.269 0.78769
prizeShare 0.0043755 0.0106711 0.410 0.68188
age_of_award -0.0021812 0.0007091 -3.076 0.00216 **
year:categoryeconomics 0.0015127 0.0016331 0.926 0.35455
year:categoryliterature 0.0015672 0.0008090 1.937 0.05302 .
year:categorymedicine 0.0008346 0.0006986 1.195 0.23251
year:categorypeace 0.0019795 0.0008215 2.410 0.01616 *
year:categoryphysics 0.0001686 0.0006788 0.248 0.80394
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2377 on 951 degrees of freedom
Multiple R-squared: 0.1006, Adjusted R-squared: 0.08826
F-statistic: 8.178 on 13 and 951 DF, p-value: 9.027e-16
While there was a visible increase in gender representation over time, it appears to be statistically insignificant when assessed across all categories by year, with some intriguing exceptions and caveats within specific domains. Notably, a more nuanced pattern surfaces when considering the individual categories. Literature and peace recipients, in particular, emerge as statistically more likely to be women. However, the significance becomes even more pronounced when the variable of the year is factored in conjunction with these categories. This nuance result suggests that not only do certain categories inherently increase the likelihood of women being recipients, but this influence also reflects an increase in the number of women winning awards in these categories over time.
The statistical significance observed in literature and peace categories, especially when considering the temporal aspect, challenges the expectations set by previous visualizations. It implies that the effect of category plays a substantial role, overshadowing the anticipated trends suggested by the graph’s increase by year in the modern era. This discrepancy underscores the complexity of gender representation dynamics, highlighting that statistical significance may manifest in unexpected ways.
To further contextualize the category values in our model, it’s crucial to establish that all comparisons are anchored against the chemistry category which acts as a benchmark. This benchmarking strategy allows for a more nuanced interpretation of the results, providing a comparative lens to assess the relative impact of each category on gender representation.
Bootstrapping Means
Having discerned notable trends across the temporal dimension, I would like to take a step back and shift the focus onto the categories, irrespective of chronological order. To achieve this, I propose adopting a bootstrap approach for the rest of the paper. Bootstrapping, a method that entails resampling data to derive sample means of gender representation across all years, aims to unveil the all-time averages and distribution of gender representation, offering a holistic perspective that transcends time-based analysis.
The motivation behind the use of bootstrapping lies in its potential to extract the true gender representation within the dataset even while the sample size is low. This approach not only mitigates the influence of temporal fluctuations but also provides a strong foundation for comparison, allowing us to gauge the persistent gender dynamics and encapsulate the underlying patterns and trends across categories
The subsequent step involves the execution of the bootstrapping code, wherein we’ll iteratively sample from the data, compute the sample means, and aggregate these results to form a comprehensive dataset. Following this, the results will be graphically presented using a boxplot, a visual tool that effectively conveys the central tendency, spread, and potential outliers within the data.
The graph depicting bootstrapped means provides a nuanced and comprehensive perspective on the distributions of values by category, offering a valuable tool for comparison. Mirroring the insights gleaned from the analysis of gender representation over time, it becomes evident that peace and literature categories consistently exhibit the highest women representation when compared to other domains. The visual delineation between two groups with one with higher representation and the other with lower becomes noticeable here too. The aforementioned categories constitute one group with an approximate 15% representation between them, while the remaining categories coalesce around a roughly 4% female representation.
This stark dichotomy in gender representation among Nobel Prize categories is a striking revelation, demarcating two distinct groups with significant differences. It is noteworthy, however, that even within the higher representation group, characterized by peace and literature, the 15% representation constituted a considerable gender gap, particularly given that women constitute 50% of the world’s population.
Unfortunately, the close proximity in size of most distributions within this sample potentially obscures statistically significant differences, particularly when considering differences established by a bootstrap confidence interval test. Given the current data sample, bootstrap comparisons of all the categories will be left for a future date. Addressing this limitation in future research by employing more robust sampling methods and incorporating additional data in subsequent years could enhance the precision of our analyses and unveil more subtle distinctions.
Building upon this foundation, the next analytical step involves running a statistical test to ascertain the significance of the observed differences across categories. Subsequently, the groups will be ranked based on the mean of means, providing a structured framework to discern the magnitude and impact of these disparities.
ANOVA
Leveraging the comprehensive insights gleaned from the bootstrapped means, the next analytical step involves the application of an ANOVA test. This statistical tool, akin to the chi-squared test, will be used to discern whether there is at least one Nobel Prize category whose sample mean distribution significantly deviates from the remainder of the dataset. Again, the null hypothesis represents an underlying truth that all data emanates from an identical distribution, while the alternative hypothesis would claim that at least one category is characterized by a distinct sample mean distribution.
Df Sum Sq Mean Sq F value Pr(>F)
category 5 202.4 40.48 24030 <2e-16 ***
Residuals 59994 101.1 0.00
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Distinguishing itself from other statistical tests, ANOVA tests introduce a different metric, the F-score, to fulfill a similar function to p-scores in previous tests. Like how a low p-score is indicative of significance in other tests, a low F-score in ANOVA is indicative of the rejection of the null hypothesis, or, in this case, the existence of statistical differences across categories. In this specific ANOVA model, the low F-score empowers us to confidently reject the null hypothesis, reinforcing the assertion that notable statistical differences persist across Nobel Prize categories in terms of gender representation.
This culmination of various analytical steps contributes to a robust verification of the current state of the Nobel Prize. The convergence of findings from different methodologies not only bolsters the reliability of the conclusions but also provides a comprehensive perspective on the intricate dynamics at play. As I finish with my statistical analysis, I hope that the insights garnered not only provide a snapshot of the present but also pave the way for informed discussions and inquiries into the evolving landscape of gender representation within the esteemed Nobel Prize recognition.
Category Rankings
After delving deeper into the intricate fabric of gender representation across various Nobel Prize categories, a statistical exploration was undertaken to pinpoint which fields exhibit the most and least gender diversity by value. By leveraging bootstrap means, I was able to shed light on the varying degrees of women recipients across different categories. The following list finally shows the categories ranked from the highest to the lowest percentage of women laureates:
Literature 17%: Emerging at the forefront with the highest representation of women recipients, the Literature category stands out as a beacon of gender diversity within the Nobel Prize landscape, even if having some way to go.
Peace 14%: Following closely, the Peace category earns a commendable position for its substantial representation of women recipients, reflecting the impact of individuals and movements dedicated to fostering global harmony.
Medicine 5.7%: Moving down the list, the Medicine category exhibits a moderate representation of women recipients, reflecting the strides made in recognizing their contributions to advancements in medical science.
Chemistry 4%: In the realm of Chemistry, women recipients contributed strongly, albeit with a lower percentage compared to other categories listed before.
Economics 3%: Economics, while making strides in acknowledging the accomplishments of women, demonstrates a slightly lower percentage of women recipients.
Physics 1.8%: Coming in last with the least gender representation in the categories, Physics stands out with the lowest percentage of women laureates. The data reveals a noteworthy contrast, emphasizing the underrepresentation of women in the field of Physics, which underscores the need for concerted efforts to address gender disparities.
These findings underscore the substantial disparities in gender representation across Nobel Prize categories, with Physics being particularly notable for its pronounced underrepresentation of women recipients. To further put it into perspective, it is intriguing to note that women are approximately ten times more likely to receive a Literature Nobel Prize compared to Physics. Additionally, an honorable mention is extended to the Peace category, which holds a commendable position in terms of gender diversity. As we continue to analyze and reflect on these patterns, it becomes increasingly apparent that fostering gender equality in recognition and acknowledgment remains an ongoing and vital endeavor across various academic and scientific domains.
Conclusions
After having sifted through the analysis, it becomes evident that gender representation varies significantly across different categories. Additionally, despite 2023 standing out as emblematic of a recent upswing in representation with higher percentage of women recipients, the broader trend suggests that there are no substantial statistical increases in the gender ratio over time, except for a few specific categories. There could be future work to find ways to make the underrepresented categories more flexible to change similar to peace and literature.
Over the years, the number of women recipients has exhibited relatively minimal changes on average, with only a slight dip observed in the 1980s. This is an intriguing observation and acts, with the more recent increases, as a potential emergence of a pattern where more women, possibly at later stages in their careers, are receiving well-deserved recognition. Given that Nobel laureates typically tend to be older, this trend could signify a positive shift in the gender ratio as more established women in various fields attain notable accomplishments.
While the current state of Nobel prizes reflects slow gains made by women’s movements, there’s optimism for the future. There is a reasonable expectation that the ratio of women recipients may experience a progressive increase across all categories in the coming years. As more women continue to make significant contributions to their respective fields, it is plausible that the gender balance within Nobel laureates will shift positively. This shift would then be recognizing gains made in the 1980s-2020s which are only now being reflected in the Nobel institution. The prospect of more inclusive and diverse representation in the prestigious Nobel Prize recipients is an encouraging sign for the advancement of gender equality in academia and beyond. Only time will reveal the full extent of these changes, and it will be fascinating to revisit and reassess the data two decades from now.
References
Data:
https://www.kaggle.com/datasets/sazidthe1/nobel-prize-data
Written with the help of ChatGPT:
Introduction text: https://chat.openai.com/c/ad311fbc-e32e-4e4a-a765-0d5f96f3f255
Other assistance: https://chat.openai.com/c/143eb7a9-966e-49eb-8197-28a1491e9395
Uses include writing improvements such as editing, proofreading, and idea expansion from my presentation.